Why the Aperture – Divergence Product Doesn’t Tell the Whole Story.
A true measure of the quality of a laser beam is the parameter known as M2, also referred to as a number of ‘times diffraction limited’. It describes how a beam will diverge compared to a theoretically ‘perfect’ laser beam of the same wavelength and initial size that has the lowest possible divergence given by diffraction theory. A theoretically perfect laser beam must have a Gaussian intensity distribution whereas most real laser beams do not. We therefore have to make some approximations when talking about M2. We measure the laser beam diameter as the diameter of a circle containing 1/e2 or about 87% of the power or energy and the divergence angle as the full angle of the cone containing the same power or energy. We use an ellipse to make the same figures where the beam is not nominally circular. Real lasers can have M2 values ranging from very little more than 1 (the theoretical minimum) to several tens or even hundreds. Many practical applications require the lowest possible value.
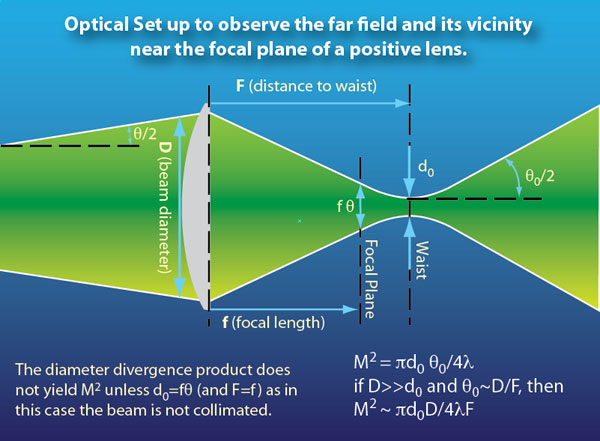
The optical set up depicted here can be used to measure both the beam divergence and the M2 value of a real laser. A lens of focal length 1 or 2m is typically used, along with attenuation optics and the beam is imaged using a CCD and software.
Measuring the beam in the focal plane of the lens yields the beam’s ‘raw’ divergence, simply by dividing the beam diameter in the focal plane by the focal length. Since we only know for sure what the laser beam diameter is near its output aperture, this figure tells us little about the beam quality. We do not know the position of the waist of the original laser beam or its size. In many real lasers, it can be located behind the laser (or sometimes well in front of it) and is thus often smaller than the laser beam diameter measured at its output aperture. Only the true waist diameter can be combined with the divergence to give M2.
By looking in the vicinity of the focal plane for a minimum diameter spot, the waist as transformed by the lens, we can gain much more useful information. For real lasers, the waist is usually located near the focal plane and usually a little way after it. Note that the original beam divergence is eliminated in the expression that gives M2. It is expressed in terms of the beam diameter at the waist, the diameter of the beam at the lens and the distance of the waist from the lens. All these parameters are relatively easily measured. The focal length of the lens and the beam diameter at the lens need to be chosen such that the waist is much smaller than the beam diameter at the lens.
Technically speaking, to achieve accurate measurements, the waist must be much greater than its Rayleigh range from the lens. This value is given by πd02/4λM2.
Beam Divergence: Irreducible and Reducible
In the discussion above, the beam divergence as measured in the focal plane of our lens frequently contains some reducible elements. These can include sphericity imposed by lensing in an amplifier after the rod (and not fully compensated by the beam expanding telescope) or sphericity resulting from improper collimation of an unstable resonator; with a fixed length and a finite number of resonator mirror curvatures, it is often impossible to achieve perfect collimation. With proper beam control after the laser, such as the transmitting optics in a LIDAR system, or the focusing lens in a machining head, this sphericity can be eliminated and the irreducible element, as predicted by M2, will determine respectively the angular resolution of the LIDAR system or the spot size at a work piece.
In some cases, our waist will be located in the focal plane of the lens. Only then can we say that the laser is truly collimated and only then can the aperture – divergence product be used to determine the beam quality. In many practical cases, this does not hold true.
The irreducible divergence (full angle) is given by the expression 4M2λ/πd where d is the diameter of the laser beam measured at its waist. For reasons given above, this figure is often lower than the ‘raw’ divergence of the laser beam itself. To a first order approximation, the above expression holds true even if the laser beam is expanded or reduced by telescopes and the like.
For more information contact Litron Lasers.